Revisiting decomposition

This a brief revisit to the idea of problem decomposition as in one of my previous posts on dual decomposition.

If you have taken a graduate level class on Bayesian Networks, or even an undergraduate class in Artificial Intelligence, then you probably remember the famous "Alarm Problem" below as a first introduction to Bayesian Networks.

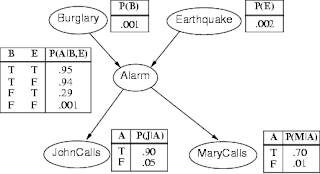
A difficulty arises in working with such networks as one tries to work with the joint probability distribution, $P(B,E,A,J,M)$, where the alphabets stand for the first letter of the

variables depicted in the network above. But the elegant property of Bayesian Networks is that the joint distribution factors multiplicatively into a number of smaller distributions, which are governed by only the relationship between a node and its parents.

For our example network, the joint distribution factors as follows:

\[ P(B,E,A,J,M) = P(J|A)P(M|A)P(A|B,E)P(B)P(E) \] which makes inference much easier to perform because of involvement of the small probability distributions.

It is amazing how the idea of decomposition pervades from relatively basic ideas in Computer Science (such as Merge Sort) to advanced techniques such as Bayesian Networks. I was trying to explain this to the undergraduate class I am a Teaching Assistant for while we were delving into Bayesian Networks for the first time. Just thought I would write a note to myself in my blog, reminding myself of the elegance of the decomposition approach to problem solving.

Topic Modeling to film scripts!

This came up during a paper discussion today in our seminar on "Statistical Models for Activity Recognition", and I wonder if someone has any ideas? Does anybody know about any work in applying topic modeling ideas (such as Latent Dirichlet Allocation (LDA) models) to film or tv scripts? I would be interested if anyone can give me pointers to such work.

Computer Scientists are evolving?

I had an interesting conversation with a friend of mine today. As both fellow computer scientists (if I may call us so), our conversations shared the general 'geekiness' inherent in a conversation among this broad class of people. One thing we realized as we were reminiscing the good old undergraduate days and trying to figure out what our other computer scientist friends are doing, is that we all think not just about `elegant coding', but are also leaning towards the concept of engineering a useful product.

It appears, at least that was our view, many computer scientists nowadays do not just go and write software for a business, but bring in new product ideas and perspective in shaping the business concept. This possibly applies mostly for technology oriented companies, but computer scientists have started to fit into the finance and advertisement industry well. The point of this rambling is that computer scientists are not just code junkies: yes, we do write software, but we are also adept in potentially translating ideas that will provide a new perspective to new areas of venture, and to develop, maybe not the next big product, but the next 'very useful' product. Computer scientists are evolving!

How trustworthy are medical device softwares?

Even though I am mostly a Machine Learning/Computer Vision/Artificial Intelligence person, I do enjoy talks in other areas of computer science or mathematics. I think it is important to have breadth in ones field, which is somewhat contradictory to the dogma of being a PhD student -- obtaining ultimate depth of knowledge and expertise in a small portion of your field of interest. Nevertheless, I pretty much go to all the "Distinguished Lecture Series" talks with a quest for understanding the cutting edge work that is going on outside my area of "expertise" (and of course, the free cookies and coffee are a good motivation as well).

Enough rambling. I got to attend a great talk by Kevin Fu on the security and privacy of medical devices (such as pacemakers) and RFID based embedded devices. He raised some very interesting points about the current state of the art in the security and privacy of such pervasive computing devices, and possible research directions to address these points. His approach appears to be based on thinking of new ways of designing the software and protocols that are effective and energy efficient. Kevin is also noted in TR 35.

Manifold Learning vs Manifold Embedding

These thoughts stem from the ambiguity that I think persists in differentiating learning vs embedding when it comes to thinking about manifold data. Any comments are welcome.

Whenever one mentions "manifold learning" in machine learning, a number of algorithms tend to pop in ones head (assuming one is familiar with this particular area in machine learning) such as Isomap, Locally Linear Embedding (LLE), Multidimensional Scaling (MDS), t-SNE, and of course, Principal Component Analysis (PCA). Generally we associate manifold learning to techniques that essentially embed very high dimensional data onto a low dimensional space (usually 2D) for purposes of visualization.

As far as I understand, these techniques generally try to build a geodesic distance map of neighborhoods for each point, and based on the distribution of such distances, construct an embedding function that maps these high dimensional points to a low dimensional space that respects these distance distributions. I am grossly simplifying the theme, but each technique builds the distribution of distances of the high dimensional points in its own way (often using an optimization formulation).

But the terminology "manifold learning" seems somewhat misleading to me. The purpose of the aforementioned techniques is more like manifold embedding; though such embedding techniques are also effective in building a recognition system, for example, I cannot fully accept the usage of "manifold learning" in describing these broad class of techniques.

Learning a manifold should entail something different. For very high dimensional data, the number of modes of variability in the data is usually far less than the number of dimensions. In other words, if one can quantify the modes of variability of the data, then one has a parametrized model that captures or describes the very high dimensional data. The learning portion is to answer the question of how one learns these variabilities. Obviously, in learning to capture these variabilities from very high dimensional data one is likely to resort to one of the many embedding techniques to make learning more tractable. Once the variabilities are learned, it can be used to embed high dimensional data into a low dimensional manifold! Being able to compactly describe a manifold might be also advantageous for classification.

In my mind, there appears to be a demarcation between the learning and the embedding views. I have not seen much work from this "learning to describe manifold" perspective. But this alternate view of manifolds might have some interesting application potential, very likely in computer vision.

Dual decomposition: a recurrent theme?

Some thoughts on the idea of decomposition; any comments or discussions are welcome.

The concept of dual decomposition for inference in graphical models, particularly MRFs, is based on an insight that resounds in almost all aspects of problem solving in computer science. The insight is the ability to decompose a very hard problem into smaller, independent problems that are solvable, and then combine these solutions in a clever way to get a solution to the original problem. The elegance of this approach is that it can be used to solve inference problems with discrete variables that result in a difficult combinatorial optimization problem.

If we think back to one of our favorite sorting algorithms (at least my favorite), mergesort, the idea of "decomposition" pervades this elegant sorting algorithm. Instead of trying to sort a large array of size $N$, break the problem up into smaller sorting problems (the divide approach), solve each of these subproblems by recursively breaking into smaller and smaller subproblems, and then combining cleverly all these solutions (the conquer approach) to the small problems to get a solution to the original sorting problem. Of course, the dual decomposition idea for inference in graphical models has its own details, but essentially one can think of it as a form of "divide and conquer".

There are many great references that I can suggest if you are interested in dual decomposition ideas for inference in graphical models. It is quite amazing that the idea of "decomposition" has not only given us efficient sorting, but has lent itself in developing very strong inference mechanisms to address difficult combinatorial optimization problems.

Epilogue: I am including a few references that give a broad overview of graphical models and the dual decomposition framework. The article by Wainwright et al. titled "Graphical Models, Exponential Families, and Variational Inference" is worth looking at. I would recommend reading the first few chapters of David Sontag's PhD thesis. Sontag, Globerson, and Jaakkola have a book chapter titled "Introduction to Dual Decomposition for Inference" that might also be of interest. Komodakis et al. have a recent PAMI article titled "MRF Energy Minimization and Beyond via Dual Decomposition" which is also a good place to look. Another recent work worth looking is by Yarkony, Ihler and Fowlkes titled "Planar Cycle Covering Graphs". All these papers have a fair bit of mathematics.

A few simple but useful .vimrc configs

I am an avid user of vim, starting from coding to writing papers in tex. I remember I got introduced to vim sometime during undergrad, and it was not very long before I switched to it from emacs. I guess I am one of those people now who believes that 'real' computer scientists use vim! Enough of retrospection, and back to the purpose of this post.

I have a few simple things set up in my .vimrc file that I have found to be quite useful over time, and thought others might just find it handy.

Useful vim 1: If you have been a computer science major as an undergrad, then the 80 character limit must have been ingrained into you. I have a very simple highlighter in my .vimrc that tells me when I am crossing over my 80 character limit per line. You can add this simple piece in your .vimrc.

match ErrorMsg '\%>80v.\+'

Useful vim 2: I have mapped keys for commenting /un-commenting blocks of code in vim in visual mode. You can set different key mappings for the different programming languages that you use. For example, here is my mapping for C++

map ,z :s/^/\/\/<TAB>/<CR>
map ,a :s/\/\/<TAB>/<CR>

Similarly for Matlab,

map ,c :s/^/%%<TAB>/<CR>
map ,d :s/%%<TAB>/<CR>

Useful vim 3: If you are like me who prefers tex to write things up, then setting up a Makefile to compile the tex from vim is a useful tool. The primary motivation for this setup is that I am too lazy to switch between terminals to compile the tex. And why should I do that when I can set up my editor. In your .vimrc, you add the following:

autocmd BufWritePost,FileWritePost *.tex !make

This basically calls make from vim when you save your tex (notice the *.tex). A very simple and generic Makefile to go with this will look something like

file.pdf: file.tex
  pdflatex file.tex
  bibtex file.aux
  pdflatex file.tex
  pdflatex file.tex

Hope these very basic vim setups will be of use.

An article on how to think

I came across this blog post by Ed Boyden last summer when I made a trip to MIT. I have been thinking of posting a link to this article for a while now; it has excellent advice for not just students but for anyone who would like to be more efficient in their work. Here is the link.

Kernel trick: feature, matrix, feature

Here is an idea for a kernel trick that might come in handy later at some point. It seems best to transfer it to this blog, instead of simply keeping it in paper, so that at a later time I can do a quick search. Here is the summary of the trick (apologies if the notation is confusing).

Suppose we have some data $x_1,x_2,\ldots,x_n$. Assume $\Psi \in \mathbb{R}^{D \times D}$. We want to write a kernel version for the form
\[ \Phi(a)^T \Psi \Phi(b) \] where $\Phi$ is a non-linear feature map for an arbitrary data point $a$.
Let $\Psi = \sum_{ij} \alpha_{ij} \Phi(x_i)\Phi(x_j)^T$. The kernel trick is as follows:
\[
\begin{align}
\Phi(a)^T \Psi \Phi(b) &= \Phi(a)^T \sum_{ij} \alpha_{ij} \Phi(x_i)\Phi(x_j)^T \Phi(b)\\
&= \sum_{ij} \alpha_{ij} \Phi(a)^T \Phi(x_i)\Phi(x_j)^T \Phi(b)\\
&= \sum_{ij} \alpha_{ij} K(a,x_i)K(x_j,b)
\end{align}
\]
This is part of a derivation to kernelize an optimization formulation. There is also an assumption here about the $\Psi$, that is, it lies in the span of our data.