A new beginning

2011 will be over in a few hours. I was thinking of making a list of what I have achieved over the last year versus what I have failed/wanted to achieve. But then again, the year will be over, and instead of possibly sulking over the seemingly daunting outcome of the aforementioned list, why not just dust yourself off and start with new energy for the new year.

Happy new year everyone! Hope you all have a great 2012...

Quick tip: colorize diff output in terminal

Just a quick and handy tip. To see diff outputs colorized in a terminal, I am using the colordiff package. Colordiff is a wrapper around diff that produces the same output as diff, except that it augments the output using colored syntax highlighting to increase readability.

So if you are using svn as your repository, you can perform svn diff | colordiff to see the colored diff output.

New blog layout

I have decided to try a new layout for my blog. If you came here randomly or have been following my blog, either way, please let me know if you like this layout...

Using mercurial (hg) for local development

Decentralized Version Control (DVCS) is one of the most useful tools if you are working with multiple people on a project. I used to use version control (such as subversion and git) to not only keep track of code for my research, but also while drafting papers. At work, we use subversion (svn) to maintain our large codebase, but having local versioning is very helpful while developing features. For local version control, I have been using mercurial (hg), which by the way is quite easy to use, and personally I think feels like a mix of svn and git.

When you check out a copy of a codebase from your project's svn trunk, for example, and you decide you want to add a new feature, branching is the way to go and the quick learning curve of mercurial will help get you started.

When you initially add all your files to mercurial, it becomes the "default" branch. For every feature you are going to develop, you can create a new branch and tag it with a name (say "feature1"). You can switch to the "default" branch when there is new code pushed into the central svn repository and you need to do an "svn up"; you can add remove any new files for mercurial and then simply merge it back with your "feature 1" mercurial branch (of course resolving any conflicts). Once "feature1" is complete after all the code reviews and everything that gets needed done, just switch to the "default" mercurial branch, make sure it is updated, and merge your "feature1" branch with it. You can push in your added feature via svn to trunk, and close off the mercurial "feature1" branch.

The basic idea is simply to use named feature branches to work on your new features, and use the default branch to perform updates, propagating to your working branches, and when you are ready to check in your newly developed feature to codebase.

Using mercurial locally on top of a checked out svn repository has been working quite well for me. So I wanted to quickly share, without actually showing you the nitty gritty details, how you might go about using a similar versioning workflow. Maybe in a later post I will sketch out the details with the mercurial commands.

A retrospection on transition to industry

I have been working in the software industry for about a month now. So I thought this might be a good time to put down some of my thoughts in writing. To summarize, the transition to industry has been a very good learning experience so far.

Honestly, I am a complete newbie in industry. I did not even have an internship experience in industry before I took off from the Phd program. Although, I did have experience working on a large scale software project that helps scientists/researchers to perform large scale data analysis as part of an academic research experience, but working on software that gets deployed to production and, hopefully, reaps some profits in is a very different world. My experiences have been broadly in academia and in research in the past, and though my proficiency in various programming languages are more than adequate, after starting work in industry as a colleague with industry experts, I realized that there are many things for me yet to learn.

I have picked up a lot of things in a month, especially the myriad set of tools that are used to streamline the whole development to production process. I definitely have a much broader perspective on software now, and coupled with my background in research and academia, I feel more complete as a professional. My startup stint might have been the missing piece to my goal of becoming an accomplished computer scientist.

f8

I was at work when f8 started today in the morning. But I did get glimpses of the live presentation showing some of the new technologies that Facebook is planning on rolling out. I think they have some very interesting products in mind, such as Timeline, Ticker, and the concept of Open graph.

The proposed changes seem intriguing, but I wonder how this will affect the nature of social networks. There is the technology aspect of the products, but I am more concerned about the type of privacy features that are getting bundled with these ideas.

Code coverage plugin for eclipse

I needed a code coverage tool to check how good of a coverage my unit tests were doing. Looking around a little for a code coverage tool for eclipse, I came across ecobertura. I only played around a little with this, but from first looks, it seems quite handy. It gives you a nice highlighting of green for lines of code that got executed, and others in red. There are some other features that I did not get a chance to check out yet. One problem is that there is no way to toggle off the code coverage tool, probably something the author has in mind to add I am sure.

If you decide to use it, please let me know how it goes for you in the meantime.

Vim like editing for eclipse

I am using eclipse at work for development, and although eclipse provides many excellent functionalities, being a vi/vim person myself, I was missing the elegance of developing using a vim style editor. One of the senior engineers at work, being himself an avid vi/vim user as myself, pointed out an eclipse plugin for vim called vrapper. It is not complete vim, but has enough functionality to keep me happy. I have been using it for about a week now, and I am liking the eclipse functionality with a vim style editor.

You can install it from eclipse marketplace. If you are using one of the relatively newer eclipse IDEs, you should see a link from "help".

Computational Advertising class @ Stanford

Since I have decided to dabble into the problem of ad serving, I have been looking at this class at Stanford trying to get a sense of what is out there currently in the real world, and what are the lines of thought of researchers in the field. Here's the link if you are interested.

A brief detour

For those of you who might have stumbled upon my blog previously, you would probably remember me as a PhD student in Machine Learning in California. I have decided to take a detour from my PhD program for a stint as a Software Engineer. I am working in California, primarily focusing in applying Machine Learning in building high value scalable products for users, and with a goal in distributing them at a massive scale.

At the moment, I have decided to delve into the problem of Ad Serving. All of us engineers in this area are basically working on the problem of how to connect advertisers, publishers, and users in a manner that is profitable for all involved, and to do all that in an efficient manner.

How are our algorithms surviving in the stock market?

With the current high volatility of stock prices, I wonder how algorithms predicting stock prices are surviving. The ups and downs over the last few days have been pretty significant, and the robustness of algorithmic predictions, in general, is something that I am curious about. From a machine learning perspective, I am interested in knowing how such techniques are surviving in the current harsh world of stock market.

Anybody has any ideas on this matter?

Interesting TED talk on how algorithms are creeping into our lives

My post on "Prelude to postings again" has been over a month old. In the spirit of blogging, here is an interesting TED talk on how algorithms are becoming a part of our daily life. People in data mining might find this talk especially attractive.

Prelude to postings again

After the digression from posting for the past few days, I am coming back again. I have been busy finishing up a masters thesis, with all its logistics, and dealing with the end of quarter in about a week. My thesis is done and turned in. I heard back from UAI; our paper got in! I also have a work at CVPR. For the next few weeks, I will be occupied working on preparing for these conferences. I have a number of things in mind that I want to talk about in the blog, and they will be coming soon. Keep tuned!

Revisiting decomposition

This a brief revisit to the idea of problem decomposition as in one of my previous posts on dual decomposition.

If you have taken a graduate level class on Bayesian Networks, or even an undergraduate class in Artificial Intelligence, then you probably remember the famous "Alarm Problem" below as a first introduction to Bayesian Networks.

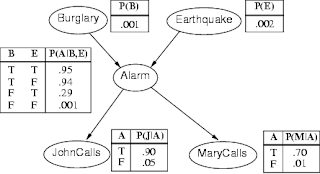
A difficulty arises in working with such networks as one tries to work with the joint probability distribution, $P(B,E,A,J,M)$, where the alphabets stand for the first letter of the

variables depicted in the network above. But the elegant property of Bayesian Networks is that the joint distribution factors multiplicatively into a number of smaller distributions, which are governed by only the relationship between a node and its parents.

For our example network, the joint distribution factors as follows:

\[ P(B,E,A,J,M) = P(J|A)P(M|A)P(A|B,E)P(B)P(E) \] which makes inference much easier to perform because of involvement of the small probability distributions.

It is amazing how the idea of decomposition pervades from relatively basic ideas in Computer Science (such as Merge Sort) to advanced techniques such as Bayesian Networks. I was trying to explain this to the undergraduate class I am a Teaching Assistant for while we were delving into Bayesian Networks for the first time. Just thought I would write a note to myself in my blog, reminding myself of the elegance of the decomposition approach to problem solving.

Topic Modeling to film scripts!

This came up during a paper discussion today in our seminar on "Statistical Models for Activity Recognition", and I wonder if someone has any ideas? Does anybody know about any work in applying topic modeling ideas (such as Latent Dirichlet Allocation (LDA) models) to film or tv scripts? I would be interested if anyone can give me pointers to such work.

Computer Scientists are evolving?

I had an interesting conversation with a friend of mine today. As both fellow computer scientists (if I may call us so), our conversations shared the general 'geekiness' inherent in a conversation among this broad class of people. One thing we realized as we were reminiscing the good old undergraduate days and trying to figure out what our other computer scientist friends are doing, is that we all think not just about `elegant coding', but are also leaning towards the concept of engineering a useful product.

It appears, at least that was our view, many computer scientists nowadays do not just go and write software for a business, but bring in new product ideas and perspective in shaping the business concept. This possibly applies mostly for technology oriented companies, but computer scientists have started to fit into the finance and advertisement industry well. The point of this rambling is that computer scientists are not just code junkies: yes, we do write software, but we are also adept in potentially translating ideas that will provide a new perspective to new areas of venture, and to develop, maybe not the next big product, but the next 'very useful' product. Computer scientists are evolving!

How trustworthy are medical device softwares?

Even though I am mostly a Machine Learning/Computer Vision/Artificial Intelligence person, I do enjoy talks in other areas of computer science or mathematics. I think it is important to have breadth in ones field, which is somewhat contradictory to the dogma of being a PhD student -- obtaining ultimate depth of knowledge and expertise in a small portion of your field of interest. Nevertheless, I pretty much go to all the "Distinguished Lecture Series" talks with a quest for understanding the cutting edge work that is going on outside my area of "expertise" (and of course, the free cookies and coffee are a good motivation as well).

Enough rambling. I got to attend a great talk by Kevin Fu on the security and privacy of medical devices (such as pacemakers) and RFID based embedded devices. He raised some very interesting points about the current state of the art in the security and privacy of such pervasive computing devices, and possible research directions to address these points. His approach appears to be based on thinking of new ways of designing the software and protocols that are effective and energy efficient. Kevin is also noted in TR 35.

Manifold Learning vs Manifold Embedding

These thoughts stem from the ambiguity that I think persists in differentiating learning vs embedding when it comes to thinking about manifold data. Any comments are welcome.

Whenever one mentions "manifold learning" in machine learning, a number of algorithms tend to pop in ones head (assuming one is familiar with this particular area in machine learning) such as Isomap, Locally Linear Embedding (LLE), Multidimensional Scaling (MDS), t-SNE, and of course, Principal Component Analysis (PCA). Generally we associate manifold learning to techniques that essentially embed very high dimensional data onto a low dimensional space (usually 2D) for purposes of visualization.

As far as I understand, these techniques generally try to build a geodesic distance map of neighborhoods for each point, and based on the distribution of such distances, construct an embedding function that maps these high dimensional points to a low dimensional space that respects these distance distributions. I am grossly simplifying the theme, but each technique builds the distribution of distances of the high dimensional points in its own way (often using an optimization formulation).

But the terminology "manifold learning" seems somewhat misleading to me. The purpose of the aforementioned techniques is more like manifold embedding; though such embedding techniques are also effective in building a recognition system, for example, I cannot fully accept the usage of "manifold learning" in describing these broad class of techniques.

Learning a manifold should entail something different. For very high dimensional data, the number of modes of variability in the data is usually far less than the number of dimensions. In other words, if one can quantify the modes of variability of the data, then one has a parametrized model that captures or describes the very high dimensional data. The learning portion is to answer the question of how one learns these variabilities. Obviously, in learning to capture these variabilities from very high dimensional data one is likely to resort to one of the many embedding techniques to make learning more tractable. Once the variabilities are learned, it can be used to embed high dimensional data into a low dimensional manifold! Being able to compactly describe a manifold might be also advantageous for classification.

In my mind, there appears to be a demarcation between the learning and the embedding views. I have not seen much work from this "learning to describe manifold" perspective. But this alternate view of manifolds might have some interesting application potential, very likely in computer vision.

Dual decomposition: a recurrent theme?

Some thoughts on the idea of decomposition; any comments or discussions are welcome.

The concept of dual decomposition for inference in graphical models, particularly MRFs, is based on an insight that resounds in almost all aspects of problem solving in computer science. The insight is the ability to decompose a very hard problem into smaller, independent problems that are solvable, and then combine these solutions in a clever way to get a solution to the original problem. The elegance of this approach is that it can be used to solve inference problems with discrete variables that result in a difficult combinatorial optimization problem.

If we think back to one of our favorite sorting algorithms (at least my favorite), mergesort, the idea of "decomposition" pervades this elegant sorting algorithm. Instead of trying to sort a large array of size $N$, break the problem up into smaller sorting problems (the divide approach), solve each of these subproblems by recursively breaking into smaller and smaller subproblems, and then combining cleverly all these solutions (the conquer approach) to the small problems to get a solution to the original sorting problem. Of course, the dual decomposition idea for inference in graphical models has its own details, but essentially one can think of it as a form of "divide and conquer".

There are many great references that I can suggest if you are interested in dual decomposition ideas for inference in graphical models. It is quite amazing that the idea of "decomposition" has not only given us efficient sorting, but has lent itself in developing very strong inference mechanisms to address difficult combinatorial optimization problems.

Epilogue: I am including a few references that give a broad overview of graphical models and the dual decomposition framework. The article by Wainwright et al. titled "Graphical Models, Exponential Families, and Variational Inference" is worth looking at. I would recommend reading the first few chapters of David Sontag's PhD thesis. Sontag, Globerson, and Jaakkola have a book chapter titled "Introduction to Dual Decomposition for Inference" that might also be of interest. Komodakis et al. have a recent PAMI article titled "MRF Energy Minimization and Beyond via Dual Decomposition" which is also a good place to look. Another recent work worth looking is by Yarkony, Ihler and Fowlkes titled "Planar Cycle Covering Graphs". All these papers have a fair bit of mathematics.

A few simple but useful .vimrc configs

I am an avid user of vim, starting from coding to writing papers in tex. I remember I got introduced to vim sometime during undergrad, and it was not very long before I switched to it from emacs. I guess I am one of those people now who believes that 'real' computer scientists use vim! Enough of retrospection, and back to the purpose of this post.

I have a few simple things set up in my .vimrc file that I have found to be quite useful over time, and thought others might just find it handy.

Useful vim 1: If you have been a computer science major as an undergrad, then the 80 character limit must have been ingrained into you. I have a very simple highlighter in my .vimrc that tells me when I am crossing over my 80 character limit per line. You can add this simple piece in your .vimrc.

match ErrorMsg '\%>80v.\+'

Useful vim 2: I have mapped keys for commenting /un-commenting blocks of code in vim in visual mode. You can set different key mappings for the different programming languages that you use. For example, here is my mapping for C++

map ,z :s/^/\/\/<TAB>/<CR>
map ,a :s/\/\/<TAB>/<CR>

Similarly for Matlab,

map ,c :s/^/%%<TAB>/<CR>
map ,d :s/%%<TAB>/<CR>

Useful vim 3: If you are like me who prefers tex to write things up, then setting up a Makefile to compile the tex from vim is a useful tool. The primary motivation for this setup is that I am too lazy to switch between terminals to compile the tex. And why should I do that when I can set up my editor. In your .vimrc, you add the following:

autocmd BufWritePost,FileWritePost *.tex !make

This basically calls make from vim when you save your tex (notice the *.tex). A very simple and generic Makefile to go with this will look something like

file.pdf: file.tex
  pdflatex file.tex
  bibtex file.aux
  pdflatex file.tex
  pdflatex file.tex

Hope these very basic vim setups will be of use.

An article on how to think

I came across this blog post by Ed Boyden last summer when I made a trip to MIT. I have been thinking of posting a link to this article for a while now; it has excellent advice for not just students but for anyone who would like to be more efficient in their work. Here is the link.

Kernel trick: feature, matrix, feature

Here is an idea for a kernel trick that might come in handy later at some point. It seems best to transfer it to this blog, instead of simply keeping it in paper, so that at a later time I can do a quick search. Here is the summary of the trick (apologies if the notation is confusing).

Suppose we have some data $x_1,x_2,\ldots,x_n$. Assume $\Psi \in \mathbb{R}^{D \times D}$. We want to write a kernel version for the form
\[ \Phi(a)^T \Psi \Phi(b) \] where $\Phi$ is a non-linear feature map for an arbitrary data point $a$.
Let $\Psi = \sum_{ij} \alpha_{ij} \Phi(x_i)\Phi(x_j)^T$. The kernel trick is as follows:
\[
\begin{align}
\Phi(a)^T \Psi \Phi(b) &= \Phi(a)^T \sum_{ij} \alpha_{ij} \Phi(x_i)\Phi(x_j)^T \Phi(b)\\
&= \sum_{ij} \alpha_{ij} \Phi(a)^T \Phi(x_i)\Phi(x_j)^T \Phi(b)\\
&= \sum_{ij} \alpha_{ij} K(a,x_i)K(x_j,b)
\end{align}
\]
This is part of a derivation to kernelize an optimization formulation. There is also an assumption here about the $\Psi$, that is, it lies in the span of our data.

Resetting latex support

My old latex support setting for blogspot is not working anymore. Here's a link that nicely describes setting up latex for blogspot. If you look at the tex below, it looks very good.

Inlining: $\gamma, \zeta$

Equation environment like display:
\[
\begin{align}
K(x,x') &= \langle x,x' \rangle\\
K(x,x') &= \langle \phi(x), \phi(x') \rangle
\end{align}
\]

New Year 2011

Happy New Year to all! Hope you have a great 2011!